When we think about the performance of a database, indexing is the first thing that comes to the mind. Here, we are going to look into how database indexing works on a database. Please note that here, architectural details are described referenced to SQLite 2.x database architecture. You can find out the backend implementation of SQLite 2.5.0 with tests, which is relevant to this post from https://github.com/madushadhanushka/simple-sqlite.
Read how overall SQLite database architecture composed in this article.
What Is B-tree?
B-tree is a data structure that store data in its node in sorted order. We can represent sample B-tree as follows.
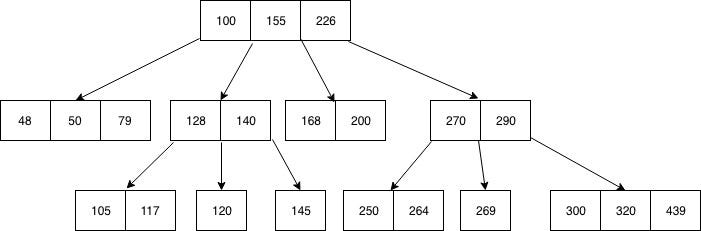 B-tree stores data such that each node contains keys in ascending order. Each of these keys has two references to another two child nodes. Te left side child node keys are less than the current keys and the right side child node keys are more than the current keys. If a single node has “n” number of keys, then it can have maximum “n+1” child nodes.
B-tree stores data such that each node contains keys in ascending order. Each of these keys has two references to another two child nodes. Te left side child node keys are less than the current keys and the right side child node keys are more than the current keys. If a single node has “n” number of keys, then it can have maximum “n+1” child nodes.
Why Is Indexing Used in the Database?
Imagine you need to store a list of numbers in a file and search a given number on that list. The simplest solution is to store data in an array and append values when new values come. But if you need to check if a given value exists in the array, then you need to search through all of the array elements one by one and check whether the given value exists. If you are lucky enough, you can find the given value in the first element. In the worst case, the value can be the last element in the array. We can denote this worst case as O(n) in asymptotic notation. This means if your array size is “n,” at most, you need to do “n” number of searches to find a given value in an array.
How could you improve this time? The easiest solution is to sort the array and use binary search to find the value. Whenever you insert a value into the array, it should maintain order. Searching start by selecting a value from the middle of the array. Then compare the selected value with the search value. If the selected value is greater than search value, ignore the left side of the array and search the value on the right side and vice versa.
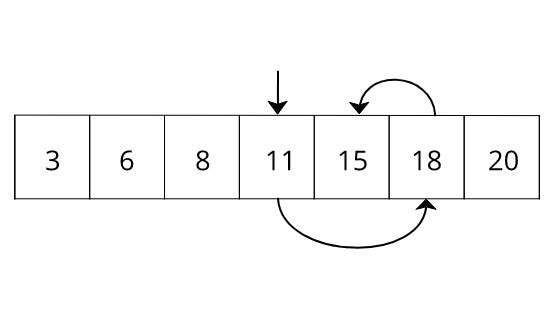 Here, we try to search key 15 from the array 3,6,8,11,15, and 18, which is already in sorted order. If you do a normal search, then it will take five units of time to search since the element is in the fifth position. But in the binary search, it will take only three searches.
Here, we try to search key 15 from the array 3,6,8,11,15, and 18, which is already in sorted order. If you do a normal search, then it will take five units of time to search since the element is in the fifth position. But in the binary search, it will take only three searches.
If we apply this binary search to all of the elements in the array, then it would be as follows.
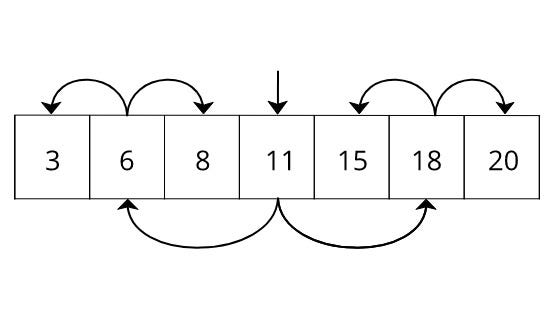
Looking familiar? It is a Binary tree. This is the simplest form of the B-tree. For Binary tree, we can use pointers instead of keeping data in a sorted array. Mathematically, we can prove that the worst case search time for a binary tree is O(log(n)). The concept of Binary tree can be extended into a more generalized form, which is known as B-tree. Instead of having a single entry for a single node, B-tree uses an array of entries for a single node and having reference to child node for each of these entries. Below are some time complexity comparisons of each pre-described method.
┌────────────────┬───────────┬────────────┬───────────┐
│ Type │ Insertion │ Deletion │ Lookup │
├────────────────┼───────────┼────────────┼───────────┤
│ Unsorted Array │ O(1) │ O(n) │ O(n) │
│ Sorted Array │ O(n) │ O(n) │ O(log(n)) │
│ Btree │ O(log(n)) │ O(log(n))) │ O(log(n)) │
└────────────────┴───────────┴────────────┴───────────┘
B+tree is another data structure that used to store data, which looks almost the same as the B-tree. The only difference of B+tree is that it stores data on the leaf nodes. This means that all non-leaf node values are duplicated in leaf nodes again. Below is a sample B+tree.
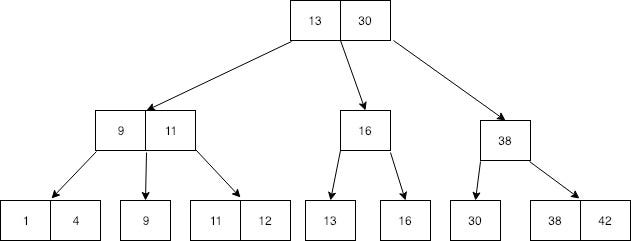 13, 30, 9, 11, 16, and 38 non-leaf values are again repeated in leaf nodes. Can you see the specialty in this tree at leaf nodes?
13, 30, 9, 11, 16, and 38 non-leaf values are again repeated in leaf nodes. Can you see the specialty in this tree at leaf nodes?
Yeah, leaf node includes all values and all of the records are in sorted order. In specialty in B+tree is, you can do the same search as B-tree, and additionally, you can travel through all the values in leaf node if we put a pointer to each leaf nodes as follows.
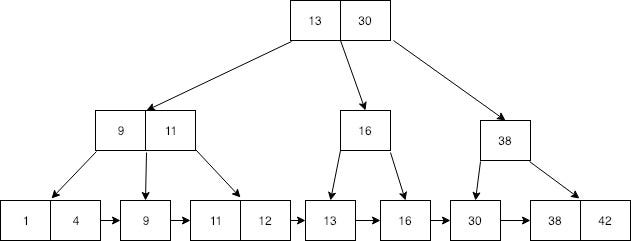 How Is Indexing Used in a Database?
When B-tree comes to the database indexing, this data structure gets a little complicated by not just having a key, but also having a value associated with the key. This value is a reference to the actual data record. The key and value together are called a payload.
How Is Indexing Used in a Database?
When B-tree comes to the database indexing, this data structure gets a little complicated by not just having a key, but also having a value associated with the key. This value is a reference to the actual data record. The key and value together are called a payload.
Assume the following three-column table needs to be stored on a database.
┌───────┬───────┬─────┐
│ Name │ Marks │ Age │
├───────┼───────┼─────┤
│ Jone │ 5 │ 28 │
│ Alex │ 32 │ 45 │
│ Tom │ 37 │ 23 │
│ Ron │ 87 │ 13 │
│ Mark │ 20 │ 48 │
│ Bob │ 89 │ 32 │
└───────┴───────┴─────┘
First, the database creates a unique random index (or primary key) for each of the given records and converts the relevant rows into a byte stream. Then, it stores each of the keys and record byte streams on a B+tree. Here, the random index used as the key for indexing. The key and record byte stream is altogether known as Payload. The resulting B+tree could be represented as follows.
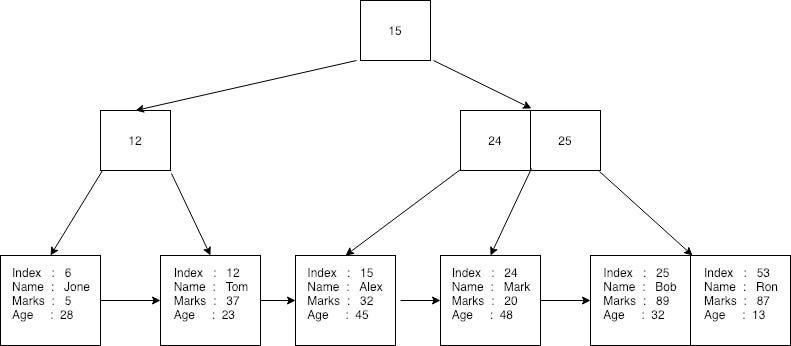 Here you can see that all records are stored in the leaf nodes of the B+tree and index used as the key to creating a B+tree. No records are stored on non-leaf nodes. Each of the leaf nodes has reference to the next record in the tree. A database can perform a binary search by using the index or sequential search by searching through every element by only traveling through the leaf nodes.
Here you can see that all records are stored in the leaf nodes of the B+tree and index used as the key to creating a B+tree. No records are stored on non-leaf nodes. Each of the leaf nodes has reference to the next record in the tree. A database can perform a binary search by using the index or sequential search by searching through every element by only traveling through the leaf nodes.
If no indexing is used, then the database reads each of these records to find the given record. When indexing is enabled, the database creates three B-trees for each of the columns in the table as follows. Here the key is the B-tree key used to indexing. The index is the reference to the actual data record.
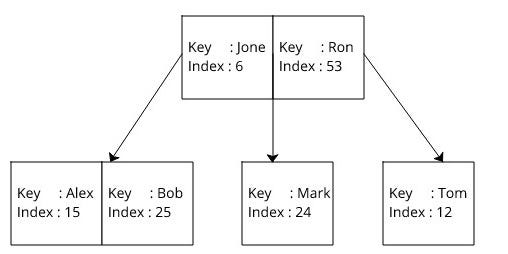 When indexing is used first, the database searches a given key in correspondence to B-tree and gets the index in O(log(n)) time. Then, it performs another search in B+tree by using the already found index in O(log(n)) time and gets the record.
When indexing is used first, the database searches a given key in correspondence to B-tree and gets the index in O(log(n)) time. Then, it performs another search in B+tree by using the already found index in O(log(n)) time and gets the record.
Each of these nodes in B-tree and B+tree is stored inside the Pages. Pages are fixed in size. Pages have a unique number starting from one. A page can be a reference to another page by using page number. At the beginning of the page, page meta details such as the rightmost child page number, first free cell offset, and first cell offset stored. There can be two types of pages in a database:
-
Pages for indexing: These pages store only index and a reference to another page.
-
Pages to store records: These pages store the actual data and page should be a leaf page.
Using SQLite B-tree indexing
The basic syntax to create a B-tree index as follows
CREATE INDEX index_name ON table_name;
There are three kinds of indexing methods used in SQLite as follows.
- Single Column Index Here, indexes are created based on one table column. Only single Btree created for indexes. Syntax as follows.
CREATE INDEX index_name ON table_name (column_name);
- Unique index Unique indexes are not allowed to store duplicate value for the column that uses indexing. Syntax can be write as follows.
CREATE UNIQUE INDEX index_name on table_name (column_name);
- Composite index This type of indexes can have multiple indexes. For each of the index column, There exist a Btree. Following is the syntax for composite index
CREATE INDEX index_name on table_name (column1, column2);
Conclusion
Databases should have an efficient way to store, read, and modify data. B-tree provides an efficient way to insert and read data. In actual Database implementation, the database uses both B-tree and B+tree together to store data. B-tree used for indexing and B+tree used to store the actual records. B+tree provides sequential search capabilities in addition to the binary search, which gives the database more control to search non-index values in a database.

